Getting started¶
Basic usage¶
Shenfun consists of classes and functions whoose purpose it is to make it easier to implement PDE’s with spectral methods in simple tensor product domains. The most important everyday tools are
A good place to get started is by creating a FunctionSpace(). There are eight families of
function spaces: Fourier, Chebyshev (first and second kind), Legendre, Laguerre, Hermite, Ultraspherical
and Jacobi.
All spaces are defined on a one-dimensional reference
domain, with their own basis functions and quadrature points. For example, we have
the regular orthogonal Chebyshev space \(\text{span}\{T_k\}_{k=0}^{N-1}\), where \(T_k\) is the
\(k\)’th Chebyshev polynomial of the first kind. To create such a function space with
8 quadrature points do:
from shenfun import FunctionSpace
N = 8
T = FunctionSpace(N, 'Chebyshev', bc=None)
Here bc=None is used to indicate that there are no boundary conditions associated
with this space, which is the default, so it could just as well have been left out.
To create
a regular orthogonal Legendre function space (i.e., \(\text{span}\{L_k\}_{k=0}^{N-1}\),
where \(L_k\) is the \(k\)’th Legendre polynomial), just replace
Chebyshev with Legendre above. And to create a Fourier function space, just use
Fourier.
The function space \(T = \text{span}\{T_k\}_{k=0}^{N-1}\) has many useful methods associated
with it, and we may experiment a little. A Function u using the basis in
\(T\) has expansion
and an instance of this function (initialized with \(\hat{u}_k=0, \, k = 0, 1, \ldots, N\)) is created in shenfun as:
from shenfun import Function
u = Function(T)
Consider now for example the polynomial \(u_e(x)=2x^2-1\), which happens to be exactly equal to \(T_2(x)\). We can create this polynomial using sympy
import sympy as sp
x = sp.Symbol('x')
ue = 2*x**2 - 1 # or simply ue = sp.chebyshevt(2, x)
The Sympy function ue can now be evaluated on the quadrature points of basis
\(T\):
from shenfun import Array
xj = T.mesh()
ua = Array(T)
ua[:] = [ue.subs(x, xx) for xx in xj]
print(xj)
[ 0.98078528 0.83146961 0.55557023 0.19509032 -0.19509032 -0.55557023
-0.83146961 -0.98078528]
print(ua)
[ 0.92387953 0.38268343 -0.38268343 -0.92387953 -0.92387953 -0.38268343
0.38268343 0.92387953]
We see that ua is an Array on the function space T, and not a
Function. The Array and Function classes
are both subclasses of Numpy’s ndarray,
and represent the two arrays associated
with a spectral Galerkin function, like (1).
The Function represents the entire spectral Galerkin function, with
array values corresponding to the sequence of expansion coefficients
\(\boldsymbol{\hat{u}}=\{\hat{u}_k\}_{k=0}^{7}\).
The Array represents the spectral Galerkin function evaluated
on the quadrature mesh of the function space T, which here is
equal to \(\{u_e(x_i)\}_{i=0}^7\).
We now want to find the Function uh corresponding to
Array ua. Considering (1), this corresponds to finding
\(\boldsymbol{\hat{u}}\) if the left hand side \(u(x_j)\) is known for
all quadrature points \(x_j\).
Since we already know that ue(x) is
equal to the second Chebyshev polynomial, we should get an array of
expansion coefficients equal to \(\boldsymbol{\hat{u}} = (0, 0, 1, 0, 0, 0, 0, 0)\).
We can compute uh either by using project() or a forward transform:
from shenfun import project
uh = Function(T)
uh = T.forward(ue, uh)
# or
# uh = ue.forward(uh)
# or
# uh = project(ue, T)
print(uh)
[-1.38777878e-17 6.72002101e-17 1.00000000e+00 -1.95146303e-16
1.96261557e-17 1.15426347e-16 -1.11022302e-16 1.65163507e-16]
So we see that the projection works to machine precision.
The projection is mathematically: find \(u_h \in T\), such that
where \(v\) is a test function, \(u_h\) is a trial function and the notation \((\cdot, \cdot)_w\) was introduced in (4). Using now \(v=T_k\) and \(u_h=\sum_{j=0}^7 \hat{u}_j T_j\), we get
for \(k = 0, 1, \ldots, 7\). This can be rewritten on matrix form as
where \(b_{kj} = (T_j, T_k)_w\), \(\tilde{u}_k = (u_e, T_k)_w\) and
summation is implied by the repeating \(j\) indices. Since the
Chebyshev polynomials are orthogonal the mass matrix \(B=(b_{kj}) \in \mathbb{R}^{N \times N}\)
is diagonal. We can assemble both the matrix \(B\) and the vector
\(\boldsymbol{\tilde{u}}=(\tilde{u}_j) \in \mathbb{R}^N\) with shenfun, and at the
same time introduce the TestFunction, TrialFunction classes
and the inner() function:
from shenfun import TestFunction, TrialFunction, inner
u = TrialFunction(T)
v = TestFunction(T)
B = inner(u, v)
u_tilde = inner(ue, v)
dict(B)
{0: array([3.14159265, 1.57079633, 1.57079633, 1.57079633, 1.57079633,
1.57079633, 1.57079633, 1.57079633])}
print(u_tilde)
[-4.35983562e-17 1.05557843e-16 1.57079633e+00 -3.06535096e-16
3.08286933e-17 1.81311282e-16 -1.74393425e-16 2.59438230e-16]
The inner() function represents the (weighted) inner product and it expects
one test function, and possibly one trial function. If, as here, it also
contains a trial function, then a matrix is returned. If inner()
contains one test, but no trial function, then an array is returned.
Finally, if inner() contains no test nor trial function, but instead
a number and an Array, like:
a = Array(T, val=1)
print(inner(1, a))
2.0
then inner() represents a non-weighted integral over the domain.
Here it returns the length of the domain (2.0) since a is initialized
to unity.
Note that the matrix \(B\) assembled above is stored using shenfun’s
SpectralMatrix class, which is a subclass of Python’s dictionary,
where the keys are the diagonals and the values are the diagonal entries.
The matrix \(B\) is seen to have only one diagonal (the principal)
\((b_{ii})_{i=0}^{7}\).
With the matrix comes a solve method and we can solve for \(\hat{u}\) through:
u_hat = Function(T)
u_hat = B.solve(u_tilde, u=u_hat)
print(u_hat)
[-1.38777878e-17 6.72002101e-17 1.00000000e+00 -1.95146303e-16
1.96261557e-17 1.15426347e-16 -1.11022302e-16 1.65163507e-16]
which obviously is exactly the same as we found using project()
or the T.forward function.
Note that Array merely is a subclass of Numpy’s ndarray,
whereas Function is a subclass
of both Numpy’s ndarray and the BasisFunction class. The
latter is used as a base class for arguments to bilinear and linear forms,
and is as such a base class also for TrialFunction and
TestFunction. An instance of the Array class cannot
be used in forms, except from regular inner products of numbers or
test function vs an Array. To illustrate, lets create some forms,
where all except the last one is ok:
from shenfun import Dx
T = FunctionSpace(12, 'Legendre')
u = TrialFunction(T)
v = TestFunction(T)
uf = Function(T)
ua = Array(T)
A = inner(v, u) # Mass matrix
c = inner(v, ua) # ok, a scalar product
d = inner(v, uf) # ok, a scalar product (slower than above)
e = inner(1, ua) # ok, non-weighted integral of ua over domain
df = Dx(uf, 0, 1) # ok
da = Dx(ua, 0, 1) # Not ok
AssertionError Traceback (most recent call last)
<ipython-input-14-3b957937279f> in <module>
----> 1 da = inner(v, Dx(ua, 0, 1))
~/MySoftware/shenfun/shenfun/forms/operators.py in Dx(test, x, k)
82 Number of derivatives
83 """
---> 84 assert isinstance(test, (Expr, BasisFunction))
85
86 if isinstance(test, BasisFunction):
AssertionError:
So it is not possible to perform operations that involve differentiation
(Dx represents a partial derivative) on an
Array instance. This is because the ua does not contain more
information than its values and its TensorProductSpace. A BasisFunction
instance, on the other hand, can be manipulated with operators like div()
grad() in creating instances of the Expr class, see
Operators.
Note that any rules for efficient use of Numpy ndarrays, like vectorization,
also applies to Function and Array instances.
Operators¶
Operators act on any single instance of a BasisFunction, which can
be Function, TrialFunction or TestFunction. The
implemented operators are:
Operators are used in variational forms assembled using inner()
or project(), like:
A = inner(grad(u), grad(v))
which assembles a stiffness matrix A. Note that the two expressions fed to
inner must have consistent rank. Here, for example, both grad(u) and
grad(v) have rank 1 of a vector.
Boundary conditions¶
The FunctionSpace() has a keyword bc that can be used to specify
boundary conditions. This keyword can take several different inputs. The
default is None, which will return an orthogonal space with no boundary
condition associated. This means for example a pure orthogonal Chebyshev
or Legendre series, if these are the families. Otherwise, a Dirichlet space
can be chosen using either one of:
bc = (a, b)
bc = {'left': {'D': a}, 'right': {'D': b}}
bc = f"u(-1)={a} && u(1)={b}"
This sets a Dirichlet boundary condition on both left and right hand side
of the domain, with a and b being the values. The third option uses the
location of the boundary, so here the domain is the standard reference domain
(-1, 1). Similarly, a pure Neumann space may be chosen using either:
bc = {'left': {'N': a}, 'right': {'N': b}}
bc = f"u'(-1)={a} && u'(1)={b}"
Using either one of:
bc = (None, b)
bc = {'right': {'D': b}}
bc = f"u(1)={b}"
returns a space with only one Dirichlet boundary condition, on the right
hand side of the domain. For one Dirichlet boundary condition on the
left instead use bc = (a, None), bc = {'left': {'D': a}} or
bc = f"u(-1)={a}".
Using either one of:
bc = (a, b, c, d)
bc = {'left': {'D': a, 'N': b}}, 'right': {'D': c, 'N': d}}
bc = f"u({-1})={a} && u'(-1)={b} && u(1)={c} && u'(1)={d}"
returns a space with 4 boundary conditions (biharmonic), where a and b
are the Dirichlet and Neumann values on the left boundary, whereas c and d
are the values on right.
The Laguerre basis is used to solve problems on the half-line \(x \in [0, \infty)\). For this family you can only specify boundary conditions at the left boundary. However, the Poisson equation requires only one condition, and the biharmonic problem two. The solution is automatically set to zero at \(x \rightarrow \infty\).
Any kind of boundary condition may be specified. For higher order
derivatives, use the form bc = f"u''(-1)={a}", or bc = {'left': {'N2': a}},
and similar for higher order.
Multidimensional problems¶
As described in the introduction, a multidimensional problem is handled using
tensor product spaces, that have basis functions generated from taking the
outer products of one-dimensional basis functions. We
create tensor product spaces using the class TensorProductSpace:
N, M = (12, 16)
C0 = FunctionSpace(N+2, 'L', bc=(0, 0), scaled=True)
K0 = FunctionSpace(M, 'F', dtype='d')
T = TensorProductSpace(comm, (C0, K0))
Associated with this is a Cartesian domain \([-1, 1] \times [0, 2\pi)\). We use
classes Function, TrialFunction and TestFunction
exactly as before:
u = TrialFunction(T)
v = TestFunction(T)
A = inner(grad(u), grad(v))
However, now A will be a tensor product matrix, or more correctly,
the sum of two tensor product matrices. This can be seen if we look at
the equations beyond the code. In this case we are using a composite
Legendre basis for the first direction and Fourier exponentials for
the second, and the tensor product basis function is
where \(\imath=\sqrt{-1}\), \(L_k\) is the \(k\)’th Legendre polynomial and \(\psi_k = (L_k-L_{k+2})/\sqrt{4k+6}\) is used for simplicity in later expressions. The trial function is now
where the sum on the Fourier exponentials will be implemented to take advantage of the Hermitian symmetry of the real input data. That is, \(\hat{u}_{k,l} = \overline{\hat{u}}_{k,-l}\), where the overline represents a complex conjugate. Note that because of this symmetry the shape of the stored array \((\hat{u}_{kl})\) will be \(N \times M/2+1\).
The inner product (inner(grad(u), grad(v))) is now computed as
where \(\overline{v}\) is the complex conjugate of \(v\) and we use the weight \(\omega = 1/2\pi\). We see that the inner product is really the sum of two tensor product matrices. However, each one of these also contains the outer product of smaller matrices. To see this we need to insert for the trial and test functions (using \(v_{mn}\) for test):
where \(A = (a_{mk}) \in \mathbb{R}^{N \times N}\) and \(B = (b_{nl}) \in \mathbb{R}^{(M/2+1)\times (M/2+1)}\),
again using the Hermitian symmetry to reduce the shape of the Fourier axis to \(M/2+1\).
The tensor product matrix \(a_{mk} b_{nl}\) (or in matrix notation \(A \otimes B\))
is the first item of the two
items in the list that is returned by inner(grad(u), grad(v)). The other
item is of course the second term in the last line of (2):
The tensor product matrices \(a_{mk} b_{nl}\) and \(c_{mk}d_{nl}\) are both instances
of the TPMatrix class. Together they lead to linear algebra systems
like:
where \(0 \le m < N, 0 \le n \le M/2\) and \(\tilde{f}_{mn} = (v_{mn}, f)_w\) for some right hand side \(f\), see, e.g., (11). Note that an alternative formulation here is
where \(U=(\hat{u}_{kl}) \in \mathbb{R}^{N \times M/2+1}\) and
\(F = (\tilde{f}_{kl}) \in \mathbb{R}^{N \times M/2+1}\) are treated as regular matrices.
This formulation is utilized to derive efficient solvers for tensor product bases
in multiple dimensions using the matrix decomposition
method in [She94] and [She95]. In shenfun we have generic solvers
for such multi-dimensional problems that make use of Kronecker product
matrices and the vec operation.
We have
where \(\text{vec}(U) = (\hat{u}_{0,0}, \ldots, \hat{u}_{0,M/2}, \hat{u}_{1,0}, \ldots \hat{u}_{1,M/2}, \ldots, \ldots, \hat{u}_{N-1,0}, \ldots, \hat{u}_{N-1,M/2})^T\)
is a vector obtained by flattening the row-major matrix \(U\). The generic Kronecker solvers
are found in Solver2D and Solver3D for two- and three-dimensional
problems.
Note that in our case the equation system (3) can be greatly simplified since three of the submatrices (\(A, B\) and \(D\)) are diagonal. Even more, two of them equal the identity matrix
whereas the last one can be written in terms of the identity (no summation on repeating indices)
Inserting for this in (3) and simplifying by requiring that \(l=n\) in the second step, we get
Now if we keep \(l\) fixed this latter equation is simply a regular linear algebra problem to solve for \(\hat{u}_{kl}\), for all \(k\). Of course, this solve needs to be carried out for all \(l\).
Note that there is a generic solver SolverGeneric1ND available for
problems like (3), that have one Fourier space and one
non-periodic space. Another possible solver is Solver2D, which
makes no assumptions of diagonality and solves the problem using a
Kronecker product matrix. Assuming there is a right hand side function
f, the solver is created and used as:
from shenfun import la
solver = la.SolverGeneric1ND(A)
u_hat = Function(T)
f_tilde = inner(v, f)
u_hat = solver(f_tilde, u_hat)
For multidimensional problems it is possible to use a boundary condition that is a function of the computational coordinates. For example:
import sympy as sp
x, y = sp.symbols('x,y', real=True)
B0 = FunctionSpace(N, 'C', bc=((1-y)*(1+y), 0), domain=(-1, 1))
B1 = FunctionSpace(N, 'C', bc=(0, (1-x)*(1+x)), domain=(-1, 1))
T = TensorProductSpace(comm, (B0, B1))
uses homogeneous Dirichlet on two out of the four sides of the
square domain \([-1, 1]\times [-1, 1]\), at \(x=-1\)
and \(y=1\). For the side where
\(y=1\), the
boundary condition is \((1-x)(1+x)\). Note that only
\(x\) will vary along the side where \(y=1\), which is
the right hand side of the domain for B1. Also note that the
boundary condition on the square domain should match in the
corners, or else there will be severe Gibbs oscillations in
the solution. The problem with two non-periodic directions
can use the solvers Solver2D or SolverGeneric2ND,
where the latter can also take one Fourier direction in a 3D
problem.
Curvilinear coordinates¶
Shenfun can be used to solve equations using curvilinear coordinates, like polar, cylindrical and spherical coordinates. The feature was added April 2020, and is still rather experimental. The curvilinear coordinates are defined by the user, who needs to provide a map, i.e., the position vector, between new coordinates and the Cartesian coordinates. The basis functions of the new coordinates need not be orthogonal, but non-orthogonal is not widely tested so use with care. In shenfun we use non-normalized natural (covariant) basis vectors. For this reason the equations may look a little bit different than usual. For example, in cylindrical coordinates we have the position vector
where \(\mathbf{i, j, k}\) are the Cartesian unit vectors and \(r, \theta, z\) are the new coordinates. The covariant basis vectors are then
leading to
We see that \(|\mathbf{b}_{\theta}| = r\) and not unity. In shenfun you can choose to use covariant basis vectors, or the more common normalized basis vectors, that are also called physical basis vectors. These are
To choose there is a configuration parameter called basisvectors in the configuration file shenfun.yaml (see Configuration), that can be set to either covariant or normal.
A vector \(\mathbf{u}\) in the covariant basis is given as
and the vector Laplacian \(\nabla^2 \mathbf{u}\) is
which is slightly different from what you see in most textbooks, which are using the normalized basis vectors.
Note that once the curvilinear map has been created, shenfun’s operators
div(), grad() and curl() work out of the box with
no additional effort. So you do not have to implement messy equations
that look like (10) directly. Take the example with
cylindrical coordinates. The vector Laplacian can be implemented
as:
from shenfun import *
import sympy as sp
r, theta, z = psi = sp.symbols('x,y,z', real=True, positive=True)
rv = (r*sp.cos(theta), r*sp.sin(theta), z)
N = 10
F0 = FunctionSpace(N, 'F', dtype='d')
F1 = FunctionSpace(N, 'F', dtype='D')
L = FunctionSpace(N, 'L', domain=(0, 1))
T = TensorProductSpace(comm, (L, F1, F0), coordinates=(psi, rv))
V = VectorSpace(T)
u = TrialFunction(V)
du = div(grad(u))
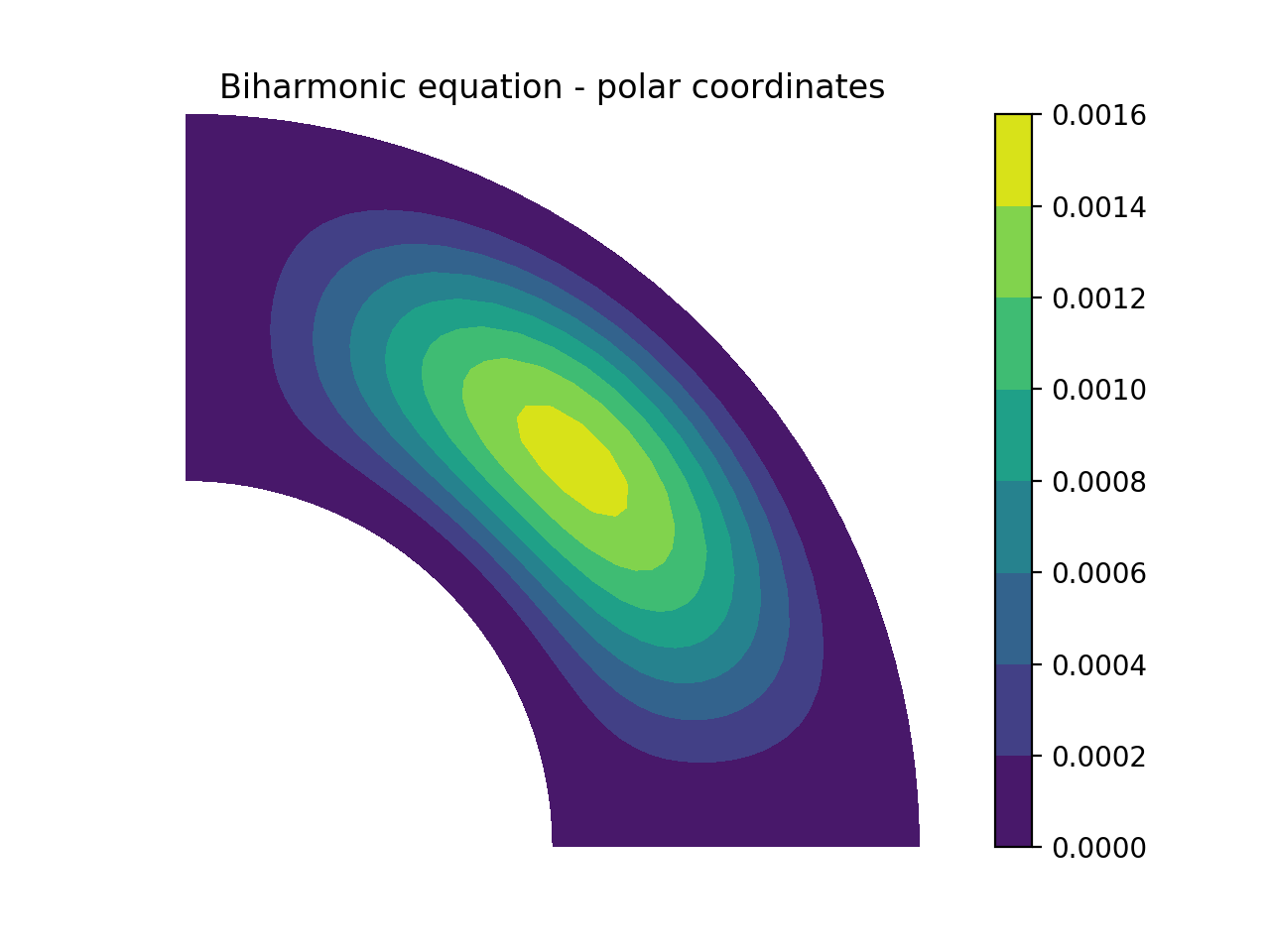
There are curvilinear demos for solving both Helmholtz’s equation and the biharmonic equation on a circular disc, a solver for 3D Poisson equation in a pipe, and a solver for the biharmonic equation on a part of the disc. Also, the Helmholtz equation solved on the unit sphere using spherical coordinates is shown here, and on the torus here. A solution from solving the biharmonic equation with homogeneous Dirichlet boundary conditions on \((\theta, r) \in [0, \pi/2] \times [0.5, 1]\) is shown below.
Coupled problems¶
With Shenfun it is possible to solve equations coupled and implicit using the
CompositeSpace class for multidimensional problems and
MixedFunctionSpace for one-dimensional problems. As an example, lets consider
a mixed formulation of the Poisson equation. The Poisson equation is given as
always as
but now we recast the problem into a mixed formulation
where we solve for the vector \(\sigma\) and scalar \(u\) simultaneously. The domain \(\Omega\) is taken as a multidimensional Cartesian product \(\Omega=(-1, 1) \times [0, 2\pi)\), but the code is more or less identical for a 3D problem. For boundary conditions we use Dirichlet in the \(x\)-direction and periodicity in the \(y\)-direction:
Note that there is no boundary condition on \(\sigma\), only on \(u\).
For this reason we choose a Dirichlet basis \(SD\) for \(u\) and a regular
Legendre or Chebyshev \(ST\) basis for \(\sigma\). With \(K0\) representing
the function space in the periodic direction, we get the relevant 2D tensor product
spaces as \(TD = SD \otimes K0\) and \(TT = ST \otimes K0\).
Since \(\sigma\) is
a vector we use a VectorSpace \(VT = TT \times TT\) and
finally a CompositeSpace \(Q = VT \times TD\) for the coupled and
implicit treatment of \((\sigma, u)\):
from shenfun import VectorSpace, CompositeSpace
N, M = (16, 24)
family = 'Legendre'
SD = FunctionSpace(N[0], family, bc=(0, 0))
ST = FunctionSpace(N[0], family)
K0 = FunctionSpace(N[1], 'Fourier', dtype='d')
TD = TensorProductSpace(comm, (SD, K0), axes=(0, 1))
TT = TensorProductSpace(comm, (ST, K0), axes=(0, 1))
VT = VectorSpace(TT)
Q = CompositeSpace([VT, TD])
In variational form the problem reads: find \((\sigma, u) \in Q\) such that
To implement this we use code that is very similar to regular, uncoupled problems. We create test and trialfunction:
gu = TrialFunction(Q)
tv = TestFunction(Q)
sigma, u = gu
tau, v = tv
and use these to assemble all blocks of the variational form (12):
# Assemble equations
A00 = inner(sigma, tau)
if family.lower() == 'legendre':
A01 = inner(u, div(tau))
else:
A01 = inner(-grad(u), tau)
A10 = inner(div(sigma), v)
Note that we here can use integration by parts for Legendre, since the weight function is a constant, and as such get the term \((-\nabla u, \tau)_w = (u, \nabla \cdot \tau)_w\) (boundary term is zero due to homogeneous Dirichlet boundary conditions).
We collect all assembled terms in a BlockMatrix:
from shenfun import BlockMatrix
H = BlockMatrix(A00+A01+A10)
This block matrix H is then simply (for Legendre)
Note that each item in (13) is a collection of instances of the
TPMatrix class, and for similar reasons as given around (4),
we get also here one regular block matrix for each Fourier wavenumber.
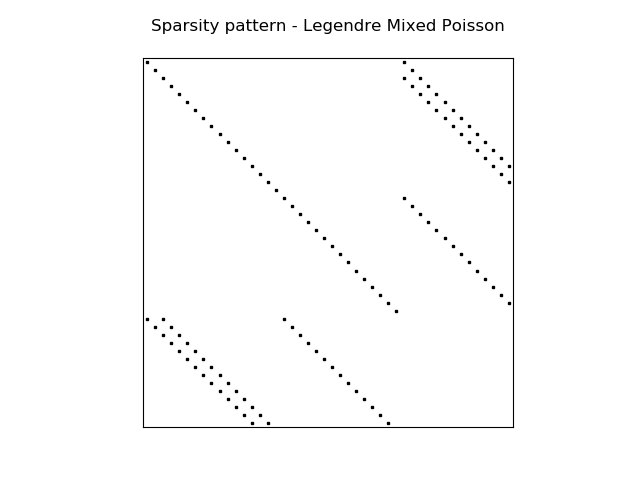
The sparsity pattern is the same for all matrices except for wavenumber 0.
The (highly sparse) sparsity pattern for block matrix \(H\) with
wavenumber \(\ne 0\) is shown in the image below
A complete demo for the coupled problem discussed here can be found in MixedPoisson.py and a 3D version is in MixedPoisson3D.py.
Integrators¶
The integrators module contains some interator classes that can be
used to integrate a solution forward in time. Integrators are set up to solve
initial value problems like
where \(u\) is the solution, \(L\) is a linear operator and \(N(u)\) is the nonlinear part of the right hand side.
There are two kinds of integrators, or time steppers. The first are ment to be subclassed and used one at the time. These are
See, e.g.:
H. Montanelli and N. Bootland "Solving periodic semilinear PDEs in 1D, 2D and
3D with exponential integrators", https://arxiv.org/pdf/1604.08900.pdf
The second kind is ment to be used for systems of equations, one class instance for each equation. These are mainly IMEX Runge Kutta integrators:
See, e.g., https://github.com/spectralDNS/shenfun/blob/master/demo/ChannelFlow.py for an example of use for the Navier-Stokes equations. The IMEX solvers are described by:
Ascher, Ruuth and Spiteri 'Implicit-explicit Runge-Kutta methods for
time-dependent partial differential equations' Applied Numerical
Mathematics, 25 (1997) 151-167
Note that the IMEX solvers are intended for use with problems consisting of one non-periodic direction.
To illustrate, we consider the time-dependent 1-dimensional Kortveeg-de Vries equation
which can also be written as
We neglect boundary issues and choose a periodic domain \([0, 2\pi)\) with Fourier exponentials as test functions. The initial condition is chosen as
where \(A\) and \(B\) are constants. For discretization in space we use the basis \(V_N = \text{span}\{exp(\imath k x)\}_{k=0}^N\) and formulate the variational problem: find \(u \in V_N\) such that
We see that the first term on the right hand side is linear in \(u\), whereas the second term is nonlinear. To implement this problem in shenfun we start by creating the necessary basis and test and trial functions
import numpy as np
from shenfun import *
N = 256
T = FunctionSpace(N, 'F', dtype='d')
u = TrialFunction(T)
v = TestFunction(T)
u_ = Array(T)
u_hat = Function(T)
We then create two functions representing the linear and nonlinear part of (14):
def LinearRHS(self, u, **params):
return -Dx(u, 0, 3)
k = T.wavenumbers(scaled=True, eliminate_highest_freq=True)
def NonlinearRHS(self, u, u_hat, rhs, **params):
rhs.fill(0)
u_[:] = T.backward(u_hat, u_)
rhs = T.forward(-0.5*u_**2, rhs)
rhs *= 1j*k
return rhs # return inner(grad(-0.5*Up**2), v)
Note that we differentiate in NonlinearRHS by using the wavenumbers k
directly. Alternative notation, that is given in commented out text, is slightly
slower, but the results are the same.
The solution vector u_ needs also to be initialized according to (15)
A = 25.
B = 16.
x = T.points_and_weights()[0]
u_[:] = 3*A**2/np.cosh(0.5*A*(x-np.pi+2))**2 + 3*B**2/np.cosh(0.5*B*(x-np.pi+1))**2
u_hat = T.forward(u_, u_hat)
Finally we create an instance of the ETDRK4 solver, and integrate
forward with a given timestep
dt = 0.01/N**2
end_time = 0.006
integrator = ETDRK4(T, L=LinearRHS, N=NonlinearRHS)
integrator.setup(dt)
u_hat = integrator.solve(u_, u_hat, dt, (0, end_time))
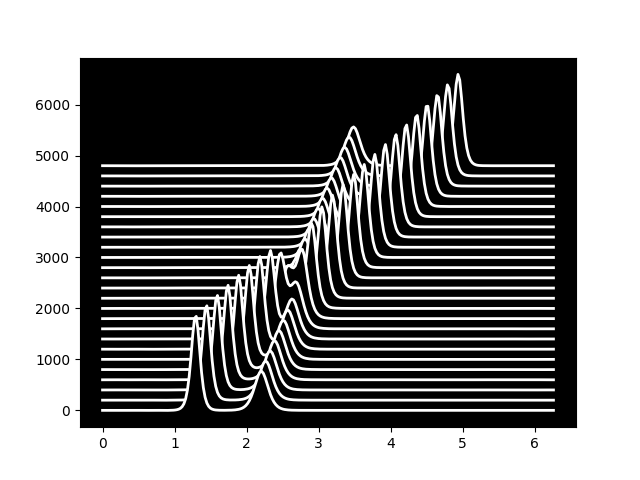
The solution is two waves travelling through eachother, seemingly undisturbed. See kdv.py for more details.
MPI¶
Shenfun makes use of the Message Passing Interface (MPI) to solve problems on distributed memory architectures. OpenMP is also possible to enable for FFTs.
Dataarrays in Shenfun are distributed using a new and completely generic method, that allows for any index of a multidimensional array to be
distributed. To illustrate, lets consider a TensorProductSpace
of three dimensions, such that the arrays living in this space will be
3-dimensional. We create two spaces that are identical, except from the MPI
decomposition, and we use 4 CPUs (mpirun -np 4 python mpitest.py, if we
store the code in this section as mpitest.py):
from shenfun import *
from mpi4py_fft import generate_xdmf
N = (20, 40, 60)
K0 = FunctionSpace(N[0], 'F', dtype='D', domain=(0, 1))
K1 = FunctionSpace(N[1], 'F', dtype='D', domain=(0, 2))
K2 = FunctionSpace(N[2], 'F', dtype='d', domain=(0, 3))
T0 = TensorProductSpace(comm, (K0, K1, K2), axes=(0, 1, 2), slab=True)
T1 = TensorProductSpace(comm, (K0, K1, K2), axes=(1, 0, 2), slab=True)
Here the keyword slab determines that only one index set of the 3-dimensional
arrays living in T0 or T1 should be distributed. The defaul is to use
two, which corresponds to a so-called pencil decomposition. The axes-keyword
determines the order of which transforms are conducted, starting from last to
first in the given tuple. Note that T0 now will give arrays in real physical
space that are distributed in the first index, whereas T1 will give arrays
that are distributed in the second. This is because 0 and
1 are the first items in the tuples given to axes.
We can now create some Arrays on these spaces:
u0 = Array(T0, val=comm.Get_rank())
u1 = Array(T1, val=comm.Get_rank())
such that u0 and u1 have values corresponding to their communicating
processors rank in the COMM_WORLD group (the group of all CPUs).
Note that both the TensorProductSpaces have functions with expansion
where \(u(x, y, z)\) is the continuous solution in real physical space, and \(\hat{u}\) are the spectral expansion coefficients. Note that the last axis has index set different from the two others because the input data is real. If we evaluate expansion (16) on the real physical mesh, then we get
The function \(u(x_i, y_j, z_k)\) corresponds to the arrays u0, u1, whereas
we have not yet computed the array \(\hat{u}\). We could get \(\hat{u}\) as:
u0_hat = Function(T0)
u0_hat = T0.forward(u0, u0_hat)
Now, u0 and u1 have been created on the same mesh, which is a structured
mesh of shape \((20, 40, 60)\). However, since they have different MPI
decomposition, the values used to fill them on creation will differ. We can
visualize the arrays in Paraview using some postprocessing tools, to be further
described in Sec Postprocessing:
u0.write('myfile.h5', 'u0', 0, domain=T0.mesh())
u1.write('myfile.h5', 'u1', 0, domain=T1.mesh())
if comm.Get_rank() == 0:
generate_xdmf('myfile.h5')
And when the generated myfile.xdmf is opened in Paraview, we
can see the different distributions. The function u0 is shown first, and
we see that it has different values along the short first dimension. The
second figure is evidently distributed along the second dimension. Both
arrays are non-distributed in the third and final dimension, which is
fortunate, because this axis will be the first to be transformed in, e.g.,
u0_hat = T0.forward(u0, u0_hat).


We can now decide to distribute not just one, but the first two axes using a pencil decomposition instead. This is achieved simply by dropping the slab keyword:
T2 = TensorProductSpace(comm, (K0, K1, K2), axes=(0, 1, 2))
u2 = Array(T2, val=comm.Get_rank())
u2.write('pencilfile.h5', 'u2', 0)
if comm.Get_rank() == 0:
generate_xdmf('pencilfile.h5')
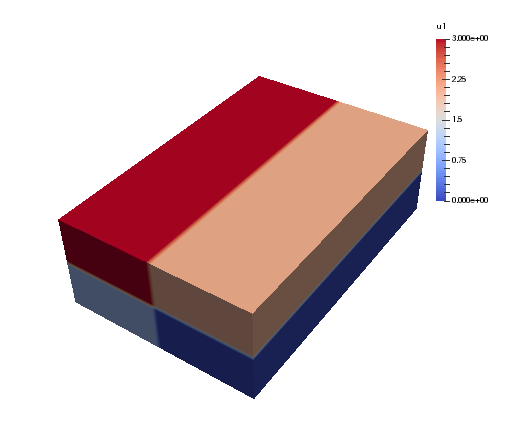
Running again with 4 CPUs the array u2 will look like:
The local slices into the global array may be obtained through:
>>> print(comm.Get_rank(), T2.local_slice(False))
0 [slice(0, 10, None), slice(0, 20, None), slice(0, 60, None)]
1 [slice(0, 10, None), slice(20, 40, None), slice(0, 60, None)]
2 [slice(10, 20, None), slice(0, 20, None), slice(0, 60, None)]
3 [slice(10, 20, None), slice(20, 40, None), slice(0, 60, None)]
In spectral space the distribution will be different. This is because the
discrete Fourier transforms are performed one axis at the time, and for
this to happen the dataarrays need to be realigned to get entire axis available
for each processor. Naturally, for the array in the pencil example
(see image), we can only perform an
FFT over the third and longest axis, because only this axis is locally available to all
processors. To do the other directions, the dataarray must be realigned and this
is done internally by the TensorProductSpace class.
The shape of the datastructure in spectral space, that is
the shape of \(\hat{u}\), can be obtained as:
>>> print(comm.Get_rank(), T2.local_slice(True))
0 [slice(0, 20, None), slice(0, 20, None), slice(0, 16, None)]
1 [slice(0, 20, None), slice(0, 20, None), slice(16, 31, None)]
2 [slice(0, 20, None), slice(20, 40, None), slice(0, 16, None)]
3 [slice(0, 20, None), slice(20, 40, None), slice(16, 31, None)]
Evidently, the spectral space is distributed in the last two axes, whereas the first axis is locally avalable to all processors. Tha dataarray is said to be aligned in the first dimension.
Post processing¶
MPI is great because it means that you can run Shenfun on pretty much
as many CPUs as you can get your hands on. However, MPI makes it more
challenging to do visualization, in particular with Python and Matplotlib.
For this reason there is a utilities module with helper classes
for dumping dataarrays to HDF5 or
NetCDF
Most of the IO has already been implemented in
mpi4py-fft.
The classes HDF5File and NCFile are used exactly as
they are implemented in mpi4py-fft. As a common interface we provide
where ShenfunFile() returns an instance of
either HDF5File or NCFile, depending on choice
of backend.
For example, to create an HDF5 writer for a 3D TensorProductSpace with Fourier bases in all directions:
from shenfun import *
from mpi4py import MPI
N = (24, 25, 26)
K0 = FunctionSpace(N[0], 'F', dtype='D')
K1 = FunctionSpace(N[1], 'F', dtype='D')
K2 = FunctionSpace(N[2], 'F', dtype='d')
T = TensorProductSpace(MPI.COMM_WORLD, (K0, K1, K2))
fl = ShenfunFile('myh5file', T, backend='hdf5', mode='w')
The file instance fl will now have two method that can be used to either write
dataarrays to file, or read them back again.
fl.write
fl.read
With the HDF5 backend we can write
both arrays from physical space (Array), as well as spectral space
(Function). However, the NetCDF4 backend cannot handle complex
dataarrays, and as such it can only be used for real physical dataarrays.
In addition to storing complete dataarrays, we can also store any slices of
the arrays. To illustrate, this is how to store three snapshots of the
u array, along with some global 2D and 1D slices:
u = Array(T)
u[:] = np.random.random(u.shape)
d = {'u': [u, (u, np.s_[4, :, :]), (u, np.s_[4, 4, :])]}
fl.write(0, d)
u[:] = 2
fl.write(1, d)
The ShenfunFile may also be used for the CompositeSpace,
or VectorSpace, that are collections of the scalar
TensorProductSpace. We can create a CompositeSpace
consisting of two TensorProductSpaces, and an accompanying writer class as:
TT = CompositeSpace([T, T])
fl_m = ShenfunFile('mixed', TT, backend='hdf5', mode='w')
Let’s now consider a transient problem where we step a solution forward in time.
We create a solution array from the Array class, and update the array
inside a while loop:
TT = VectorSpace(T)
fl_m = ShenfunFile('mixed', TT, backend='hdf5', mode='w')
u = Array(TT)
tstep = 0
du = {'uv': (u,
(u, [4, slice(None), slice(None)]),
(u, [slice(None), 10, 10]))}
while tstep < 3:
fl_m.write(tstep, du, forward_output=False)
tstep += 1
Note that on each time step the arrays
u, (u, [4, slice(None), slice(None)]) and (u, [slice(None), 10, 10])
are vectors, and as such of global shape (3, 24, 25, 26), (3, 25, 26) and
(3, 25), respectively. However, they are stored in the hdf5 file under their
spatial dimensions 1D, 2D and 3D, respectively.
Note that the slices in the above dictionaries are global views of the global arrays, that may or may not be distributed over any number of processors. Also note that these routines work with any number of CPUs, and the number of CPUs does not need to be the same when storing or retrieving the data.
After running the above, the different arrays will be found in groups stored in myh5file.h5 with directory tree structure as:
myh5file.h5/
└─ u/
├─ 1D/
| └─ 4_4_slice/
| ├─ 0
| └─ 1
├─ 2D/
| └─ 4_slice_slice/
| ├─ 0
| └─ 1
├─ 3D/
| ├─ 0
| └─ 1
└─ mesh/
├─ x0
├─ x1
└─ x2
Likewise, the mixed.h5 file will at the end of the loop look like:
mixed.h5/
└─ uv/
├─ 1D/
| └─ slice_10_10/
| ├─ 0
| ├─ 1
| └─ 3
├─ 2D/
| └─ 4_slice_slice/
| ├─ 0
| ├─ 1
| └─ 3
├─ 3D/
| ├─ 0
| ├─ 1
| └─ 3
└─ mesh/
├─ x0
├─ x1
└─ x2
Note that the mesh is stored as well as the results. The three mesh arrays are all 1D arrays, representing the domain for each basis in the TensorProductSpace.
With NetCDF4 the layout is somewhat different. For mixed above,
if we were using backend netcdf instead of hdf5,
we would get a datafile where ncdump -h mixed.nc would result in:
netcdf mixed {
dimensions:
time = UNLIMITED ; // (3 currently)
i = 3 ;
x = 24 ;
y = 25 ;
z = 26 ;
variables:
double time(time) ;
double i(i) ;
double x(x) ;
double y(y) ;
double z(z) ;
double uv(time, i, x, y, z) ;
double uv_4_slice_slice(time, i, y, z) ;
double uv_slice_10_10(time, i, x) ;
}
Note that it is also possible to store vector arrays as scalars. For NetCDF4 this is necessary for direct visualization using Visit. To store vectors as scalars, simply use:
fl_m.write(tstep, du, forward_output=False, as_scalar=True)
ParaView¶
The stored datafiles can be visualized in ParaView.
However, ParaView cannot understand the content of these HDF5-files without
a little bit of help. We have to explain that these data-files contain
structured arrays of such and such shape. The way to do this is through
the simple XML descriptor XDMF. To this end there is a
function imported from mpi4py-fft
called generate_xdmf that can be called with any one of the
generated hdf5-files:
generate_xdmf('myh5file.h5')
generate_xdmf('mixed.h5')
This results in some light xdmf-files being generated for the 2D and 3D arrays in the hdf5-file:
myh5file.xdmf
myh5file_4_slice_slice.xdmf
mixed.xdmf
mixed_4_slice_slice.xdmf
These xdmf-files can be opened and inspected by ParaView. Note that 1D arrays are not wrapped, and neither are 4D.
An annoying feature of Paraview is that it views a three-dimensional array of
shape \((N_0, N_1, N_2)\) as transposed compared to shenfun. That is,
for Paraview the last axis represents the \(x\)-axis, whereas
shenfun (like most others) considers the first axis to be the \(x\)-axis.
So when opening a
three-dimensional array in Paraview one needs to be aware. Especially when
plotting vectors. Assume that we are working with a Navier-Stokes solver
and have a three-dimensional VectorSpace to represent
the fluid velocity:
from mpi4py import MPI
from shenfun import *
comm = MPI.COMM_WORLD
N = (32, 64, 128)
V0 = FunctionSpace(N[0], 'F', dtype='D')
V1 = FunctionSpace(N[1], 'F', dtype='D')
V2 = FunctionSpace(N[2], 'F', dtype='d')
T = TensorProductSpace(comm, (V0, V1, V2))
TV = VectorSpace(T)
U = Array(TV)
U[0] = 0
U[1] = 1
U[2] = 2
To store the resulting Array U we can create an instance of the
HDF5File class, and store using keyword as_scalar=True:
hdf5file = ShenfunFile("NS", TV, backend='hdf5', mode='w')
...
file.write(0, {'u': [U]}, as_scalar=True)
file.write(1, {'u': [U]}, as_scalar=True)
Alternatively, one may store the arrays directly as:
U.write('U.h5', 'u', 0, domain=T.mesh(), as_scalar=True)
U.write('U.h5', 'u', 1, domain=T.mesh(), as_scalar=True)
Generate an xdmf file through:
generate_xdmf('NS.h5')
and open the generated NS.xdmf file in Paraview. You will then see three scalar
arrays u0, u1, u2, each one of shape (32, 64, 128), for the vector
component in what Paraview considers the \(z\), \(y\) and \(x\) directions,
respectively. Other than the swapped coordinate axes there is no difference.
But be careful if creating vectors in Paraview with the Calculator. The vector
should be created as:
u0*kHat+u1*jHat+u2*iHat